| Type: | Package |
| Title: | Precision Based Sample Size Calculation |
| Version: | 0.3.9 |
| Maintainer: | Alan G. Haynes <alan.haynes@unibe.ch> |
| Description: | Bland (2009) <doi:10.1136/bmj.b3985> recommended to base study sizes on the width of the confidence interval rather the power of a statistical test. The goal of 'presize' is to provide functions for such precision based sample size calculations. For a given sample size, the functions will return the precision (width of the confidence interval), and vice versa. |
| License: | GPL-3 |
| URL: | https://github.com/CTU-Bern/presize, https://ctu-bern.github.io/presize/ |
| BugReports: | https://github.com/CTU-Bern/presize/issues |
| Encoding: | UTF-8 |
| RoxygenNote: | 7.3.3 |
| Suggests: | binom, dplyr, ggplot2, gt, Hmisc, knitr, magrittr, markdown, rmarkdown, shinydashboard, shinytest, testthat, tidyr |
| Imports: | kappaSize (≥ 1.2), shiny |
| VignetteBuilder: | knitr |
| NeedsCompilation: | no |
| Packaged: | 2025-11-17 15:08:46 UTC; haynes |
| Author: | Armando Lenz [aut], Alan G. Haynes [cre, aut], Andreas Limacher [aut], Odile Stalder [ctb], Marie Roumet [ctb] |
| Repository: | CRAN |
| Date/Publication: | 2025-11-18 06:10:16 UTC |
presize: Precision Based Sample Size Calculation
Description

Bland (2009) doi:10.1136/bmj.b3985 recommended to base study sizes on the width of the confidence interval rather the power of a statistical test. The goal of 'presize' is to provide functions for such precision based sample size calculations. For a given sample size, the functions will return the precision (width of the confidence interval), and vice versa.
Author(s)
Maintainer: Alan G. Haynes alan.haynes@unibe.ch
Authors:
Armando Lenz
Andreas Limacher andreas.limacher@paraplegie.ch
Other contributors:
Odile Stalder odile.stalder@unibe.ch [contributor]
Marie Roumet marie.roumet@unibe.ch [contributor]
See Also
Useful links:
Report bugs at https://github.com/CTU-Bern/presize/issues
Presize shiny app
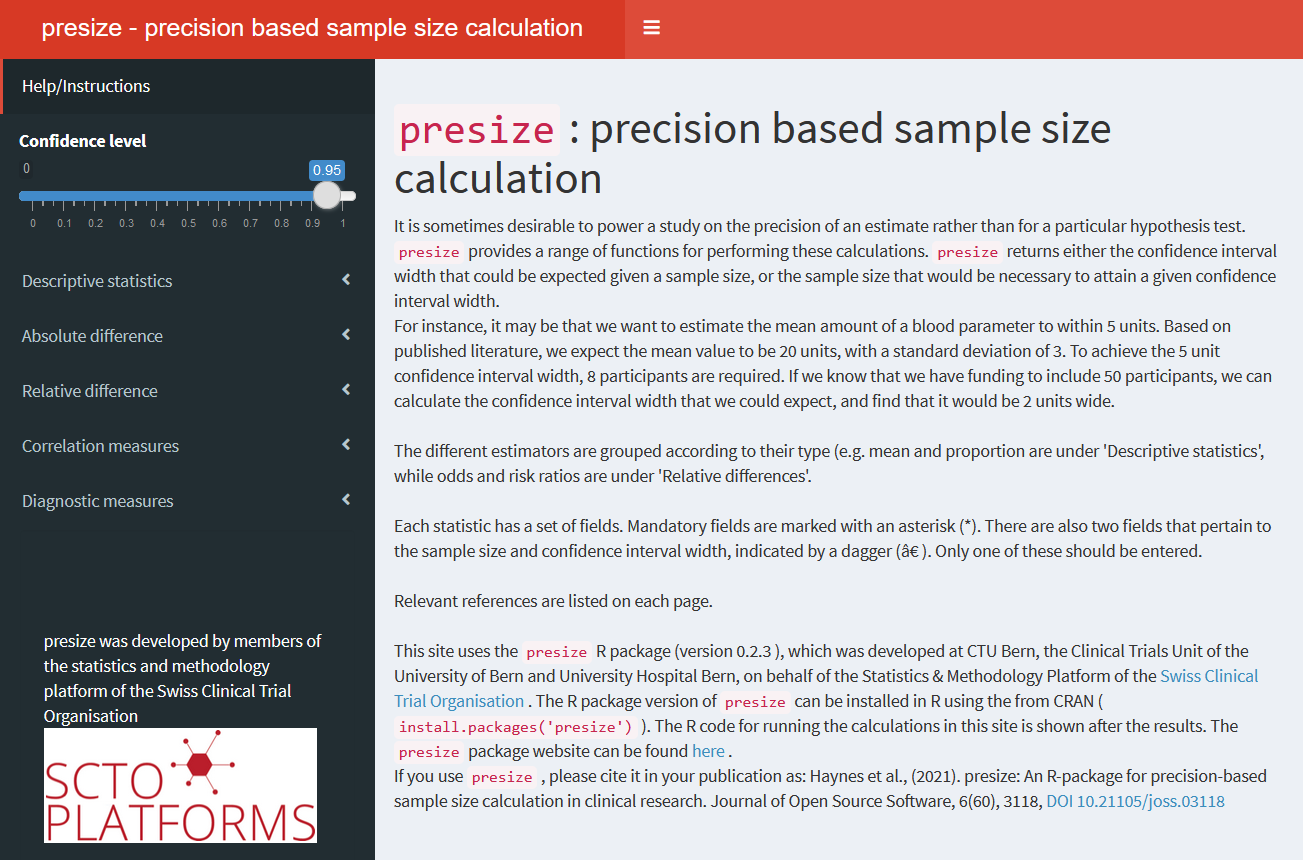
Description
Besides the programmatic approach to using presize, we also supply a shiny app, enabling point-and-click interaction with the program. The app will open in a new window. Select the appropriate method from the menu on the left and enter the relevant parameters indicated in the panel on the right. The output is then displayed lower down the page.
Usage
launch_presize_app()
Details
The main disadvantage to the app is that it only allows a single scenario at a time.
The app is also available at https://shiny.ctu.unibe.ch/presize/.
Examples
# launch the app
## Not run:
launch_presize_app()
## End(Not run)
Sample size or precision for AUC
Description
Calculate the sample size from AUC, prevalence and confidence interval width or the expected confidence interval width from AUC, prevalence and sample size, following Hanley and McNeil (1982).
Usage
prec_auc(auc, prev, n = NULL, conf.width = NULL, conf.level = 0.95, ...)
Arguments
auc |
AUC value. |
prev |
prevalence. |
n |
number of observations. |
conf.width |
precision (the full width of the confidence interval). |
conf.level |
confidence level. |
... |
other arguments to |
Details
Sample size is derived by optimizing the difference between the difference
between the lower and upper limits of the confidence interval and
conf.width.
Value
Object of class "presize", a list of arguments (including the computed one) augmented with method and note elements.
References
Hanley, JA and McNeil, BJ (1982) The Meaning and Use of the Area under a Receiver Operating Characteristic (ROC) Curve. Radiology 148, 29-36
Examples
# confidence interval width
N <- 500
prev <- .1
auc <- .65
(prec <- prec_auc(auc, prev, n = N))
cwidth <- prec$conf.width
# sample size
prec_auc(auc, prev, conf.width = cwidth)
Sample size or precision for correlation coefficient
Description
prec_cor returns the sample size or the precision for the given
pearson, spearman, or kendall correlation coefficient.
Usage
prec_cor(
r,
n = NULL,
conf.width = NULL,
conf.level = 0.95,
method = c("pearson", "kendall", "spearman"),
...
)
Arguments
r |
desired correlation coefficient. |
n |
sample size. |
conf.width |
precision (the full width of the confidence interval). |
conf.level |
confidence level. |
method |
Exactly one of |
... |
other options to uniroot (e.g. |
Details
Exactly one of the parameters n or conf.width must be passed as NULL,
and that parameter is determined from the other.
Sample size or precision is calculated according to formula 2 in Bonett and
Wright (2000). The use of pearson is only recommended, if n \ge 25. The
pearson correlation coefficient assumes bivariate normality. If the
assumption of bivariate normality cannot be met, spearman or kendall should
be considered.
n is rounded up to the next whole number using ceiling.
uniroot is used to solve n.
Value
Object of class "presize", a list of arguments (including the computed one) augmented with method and note elements.
References
Bonett DG, and Wright TA (2000) Sample size requirements for estimating Pearson, Kendall and Spearman correlations Psychometrika 65:23-28. doi:10.1007/BF02294183
Examples
# calculate confidence interval width...
# Pearson correlation coefficient
prec_cor(r = 0.5, n = 100)
# Kendall rank correlation coefficient (tau)
prec_cor(r = 0.5, n = 100, method = "kendall")
# Spearman's rank correlation coefficient
prec_cor(r = 0.5, n = 100, method = "spearman")
# calculate N required for a given confidence interval width...
# Pearson correlation coefficient
prec_cor(r = 0.5, conf.width = .15)
# Kendall rank correlation coefficient (tau)
prec_cor(r = 0.5, conf.width = .15, method = "kendall")
# Spearman's rank correlation coefficient
prec_cor(r = 0.5, conf.width = .15, method = "spearman")
Sample size or precision for Cronbach's alpha
Description
prec_cronb returns the sample size or the precision for the given
Cronbach's alpha.
Usage
prec_cronb(k, calpha, n = NULL, conf.level = 0.95, conf.width = NULL)
Arguments
k |
number of measurements/items. |
calpha |
desired Cronbach's alpha. |
n |
sample size. |
conf.level |
confidence level. |
conf.width |
precision (the full width of the confidence interval). |
Details
Exactly one of the parameters n or conf.width must be passed as NULL,
and that parameter is determined from the other.
Sample size or precision is calculated according to the formula & code and provided in Bonett and Wright (2014).
n is rounded up to the next whole number using ceiling.
Value
Object of class "presize", a list of arguments (including the computed one) augmented with method and note elements.
References
Bonett, D. G. and Wright, T. A. (2015) Cronbach's alpha reliability: Interval estimation, hypothesis testing, and sample size planning J. Organiz. Behav., 36, pages 3– 15. doi:10.1002/job.1960. # k= number of items
Examples
# calculate confidence interval width...
prec_cronb (k=5,calpha=0.7,n= 349,conf.level= 0.95, conf.width= NULL)
# calculate N required for a given confidence interval width...
prec_cronb (k=5,calpha=0.7,n= NULL,conf.level= 0.95, conf.width= 0.1)
Sample size or precision for an intraclass correlation
Description
prec_icc returns the sample size or the precision for the given
intraclass correlation.
Usage
prec_icc(rho, k, n = NULL, conf.width = NULL, conf.level = 0.95)
Arguments
rho |
desired intraclass correlation. |
k |
number of observations per n (subject). |
n |
number of subjects. |
conf.width |
precision (the full width of the confidence interval). |
conf.level |
confidence level. |
Details
Exactly one of the parameters n or conf.width must be passed as NULL,
and that parameter is determined from the others.
Sample size or precision is calculated according to formula 3 in Bonett
(2002), which is an approximation. Whether ICC is calculated for a one-way or
a two-way ANOVA does not matter in the approximation. As suggested by the
author, 5*rho is added to n, if k = 2 and rho \ge 7. This
makes the assumption that there is no interaction between rater and subject.
n is rounded up to the next whole number using ceiling.
Value
Object of class "presize", a list of arguments (including the computed one) augmented with method and note elements.
References
Bonett DG (2002). Sample size requirements for estimating intraclass correlations with desired precision. Statistics in Medicine, 21:1331-1335. doi:10.1002/sim.1108
Examples
# Bonett (2002) gives an example using 4 raters, with an ICC of 0.85 and want
# a confidence width of 0.2. Bonett calculated that a sample size of 19.2 was
# required. This can be done via
prec_icc(0.85, 4, conf.width = 0.2)
# note that \code{presamp} rounds up to the nearist integer.
# Bonett then goes on to estimate the width given the sample size, finding a
# value 'close to 0.2':
prec_icc(0.85, 4, 20)
Sample size or precision for Cohen's kappa
Description
prec_kappa returns the sample size or the precision for the provided Cohen's kappa coefficient.
Usage
prec_kappa(
kappa,
n = NULL,
raters = 2,
n_category = 2,
props,
conf.width = NULL,
conf.level = 0.95
)
Arguments
kappa |
expected value of Cohen's kappa. |
n |
sample size. |
raters |
number of raters (maximum of 6). |
n_category |
number of categories of outcomes (maximum of 5). |
props |
expected proportions of each outcome (should have length
|
conf.width |
precision (the full width of the confidence interval). |
conf.level |
confidence level. |
Details
This function wraps the FixedN and CI functions in the
kappaSize package.
The FixedN functions in kappaSize return a one sided confidence
interval. The values that are passed to kappaSize ensure that two-sided
confidence intervals are returned, although we assume that confidence intervals
are symmetrical.
Value
Object of class "presize", a list of arguments (including the computed one) augmented with method and note elements.
See Also
FixedNBinary,
FixedN3Cats,
CIBinary,
CI3Cats
Examples
# precision based on sample size
# two categories with proportions of 30 and 70\%, four raters
prec_kappa(kappa = .5, n = 200, raters = 4, n_category = 2, props = c(.3,.7))
# sample size to get a given precision
prec_kappa(kappa = .5, conf.width = .15, raters = 4, n_category = 2,
props = c(.3,.7))
# as above, but with two scenarios for kappa
prec_kappa(kappa = c(.5, .75), conf.width = .15, raters = 4, n_category = 2,
props = c(.3,.7))
prec_kappa(kappa = c(.5, .75), conf.width = c(.15, 0.3), raters = 4,
n_category = 2, props = c(.3,.7))
Sample size or precision for limit of agreement on Bland-Altman plots
Description
prec_lim_agree returns the sample size or the precision for the limit
of agreement, i.e. the confidence interval around the limit of agreement,
expressed in SD-units. It is an approximation based on the Normal distribution,
instead of a Student t distribution.
Usage
prec_lim_agree(n = NULL, conf.width = NULL, conf.level = 0.95)
Arguments
n |
sample size. |
conf.width |
precision (the full width of the confidence interval). |
conf.level |
confidence level. |
Details
Exactly one of the parameters n or conf.width must be passed as NULL,
and that parameter is determined from the other.
The sample size and precision are calculated according to formulae in Bland & Altman (1986). The CI width is a simple function of the sample size only.
Value
Object of class "presize", a list of arguments (including the computed one) augmented with method and note elements.
References
Bland & Altman (1986) Statistical methods for assessing agreement between two methods of clinical measurement Lancet i(8476):307-310 doi:10.1016/S0140-6736(86)90837-8
Examples
# calculate confidence interval width, given N
prec_lim_agree(200)
# calculate N given, confidence interval width
prec_lim_agree(conf.width = .1)
Sample size or precision for likelihood ratios
Description
These functions calculate the precision or sample size for likelihood ratios (LRs).
prec_lr is a generalized method for that can be used for positive and
negative LRs as well as conditional LRs.
prec_pos_lr is a wrapper to prec_lr to ease
calculations for positive likelihood ratios by allowing sensitivity and
specificity to be given explicitly.
prec_neg_lr is a wrapper to prec_lr to ease
calculations for negative likelihood ratios by allowing sensitivity and
specificity to be given explicitly.
Usage
prec_lr(prev, p1, p2, n = NULL, conf.width = NULL, conf.level = 0.95, ...)
prec_pos_lr(
prev,
sens,
spec,
n = NULL,
conf.width = NULL,
conf.level = 0.95,
...
)
prec_neg_lr(
prev,
sens,
spec,
n = NULL,
conf.width = NULL,
conf.level = 0.95,
...
)
Arguments
prev |
disease/case prevalence in the study group. |
p1 |
proportion of positives in group 1 (e.g. sensitivity). |
p2 |
proportion of positives in group 2 (e.g. 1 - specificity). |
n |
total group size. |
conf.width |
precision (the full width of the confidence interval). |
conf.level |
confidence level (defaults to 0.95). |
... |
other arguments to uniroot (e.g. |
sens |
sensitivity. |
spec |
specificity. |
Details
These functions implement formula 10 from Simel et al 1991.
prec_lr is a generalized function allowing for many scenarios, while
prec_pos_lr and prec_neg_lr are specific to positive and
negative likelihood ratios in the 2*2 setting (e.g. disease status and test
positive/negative).
For the positive likelihood ratio (LR+), in a 2x2 style experiment, p1
should be sensitivity, p2 should be 1-specificity. Alternatively, use
prec_pos_lr.
For the negative likelihood ratio (LR-), in a 2x2 style experiment, p1
should be 1-sensitivity, p2 should be specificity. Alternatively, use
prec_neg_lr.
For conditional likelihood ratios with 3x2 tables, such as positive or
negative tests against inconclusive ones (yields), p1 would be the
proportion of positive or negative tests in the diseased group and p2
would be the proportion of positive or negative tests in the non-diseased group.
Value
Object of class "presize", a list of arguments (including the computed one) augmented with method and note elements.
Functions
-
prec_pos_lr(): "Positive likelihood ratio" -
prec_neg_lr(): "Negative likelihood ratio"
References
Simel, DL, Samsa, GP and Matchar, DB (1991) Likelihood ratios with confidence: Sample size estimation for diagnostic test studies. J Clin Epidemiol 44(8), 763-770
Examples
# equal numbers of diseased/non-diseased, 80% sens, 73% spec, 74 participants total
prec_lr(.5, .8, .27, 74)
# Simel et al 1991, problem 1 - LR+ CI width from N
# Sensitivity of a new test is at least 80%, specificity is 73% and the LR+
# is 2.96 (= 0.8/(1-0.73)). We have as many diseased as not diseased
# (n1 = n2, n = 2*n1 = 146.8, prevalence = .5)
prec_lr(prev = .5, p1 = .8, p2 = 1-.73, n = 146.8)
prec_pos_lr(prev = .5, sens = .8, spec = .73, n = 146.8)
# problem 1 of Simel et al actually derives n1 rather than the width of the
# confidence interval (ie N from CI width). If we know that the lower limit
# of the CI should be 2.0, the confidence interval width is approximately
# exp(2*(log(2.96) - log(2))) = 2.19 (approximate because the CI Of the LR
# is only symetrical on the log(LR) scale), which we can put in conf.width
prec_lr(prev = .5, p1 = .8, p2 = 1-.73, conf.width = 2.2)
# same, but using the wrapper to specify sens and spec
prec_pos_lr(prev = .5, sens = .8, spec = .73, conf.width = 2.2)
# Simel et al 1991, problem 2 - LR- CI width from N
# p1 = 1 - sens = .1, p2 = spec = .5
# n1 = n2, n = 160, prev = .5
prec_lr(prev = .5, p1 = .1, p2 = .5, n = 160)
# same, but using the wrapper to specify sens and spec
prec_neg_lr(prev = .5, sens = .9, spec = .5, n = 160)
Sample size or precision for a mean
Description
prec_mean returns the sample size or the precision for the provided
mean and standard deviation.
Usage
prec_mean(
mean,
sd,
n = NULL,
conf.width = NULL,
conf.level = 0.95,
...,
mu = NULL
)
Arguments
mean |
mean. |
sd |
standard deviation. |
n |
number of observations. |
conf.width |
precision (the full width of the confidence interval). |
conf.level |
confidence level. |
... |
other arguments to uniroot (e.g. |
mu |
deprecated argument |
Details
Exactly one of the parameters n or conf.width must be passed as NULL,
and that parameter is determined from the other.
The precision is defined as the full width of the confidence interval. The
confidence interval calculated as t(n - 1) * sd / sqrt(n), with t(n-1)
from the t-distribution with n-1 degrees of freedom.
This function is also suitable for a difference in paired means, as this reduces to a single value per individual - the difference.
uniroot is used to solve n.
Value
Object of class "presize", a list with mean mean, sd standard deviation, n sample size,
conf.width precision (the width of the confidence interval),
lwr lower bound of confidence interval, upr upper bound of confidence interval,
augmented with method and note elements.
Examples
# mean of 5, SD of 2.5, whats the confidence interval width with 20 participants?
prec_mean(mean = 5, sd = 2.5, n = 20)
# mean of 5, SD of 2.5, how many participants for CI width of 2.34?
prec_mean(mean = 5, sd = 2.5, conf.width = 2.34) # approximately the inverse of above
Sample size or precision for a mean difference
Description
prec_meandiff returns the sample size or the precision for the
provided mean difference and standard deviations. For paired differences, use
prec_mean, as it is equivalent to a simple mean.
Usage
prec_meandiff(
delta,
sd1,
sd2 = sd1,
n1 = NULL,
r = 1,
conf.width = NULL,
conf.level = 0.95,
variance = c("equal", "unequal"),
...
)
Arguments
delta |
difference in means between the two groups. |
sd1 |
standard deviation in group 1. |
sd2 |
standard deviation in group 2. |
n1 |
number of patients in group 1. |
r |
allocation ratio (relative size of group 2 and group 1 (n2 / n1)). |
conf.width |
precision (the full width of the confidence interval). |
conf.level |
confidence level. |
variance |
|
... |
other options to uniroot (e.g. |
Details
Exactly one of the parameters n or conf.width must be passed as NULL,
and that parameter is determined from the other.
Value
Object of class "presize", a list of arguments (including the computed one) augmented with method and note elements.
Examples
# mean difference of 5, SD of 2.5, CI width with 20 participants assuming equal variances
prec_meandiff(delta = 5, sd1 = 2.5, n1 = 20, var = "equal")
# mean difference of 5, SD of 2.5, number of participants for a CI width of 3,
# assuming equal variances
prec_meandiff(delta = 5, sd1 = 2.5, conf.width = 3, var = "equal")
Sample size or precision for an odds ratio
Description
prec_or returns the sample size or the precision for the
provided proportions.
Usage
prec_or(
p1,
p2,
n1 = NULL,
r = 1,
conf.width = NULL,
conf.level = 0.95,
method = c("gart", "woolf", "indip_smooth"),
...
)
Arguments
p1 |
risk among exposed. |
p2 |
risk among unexposed. |
n1 |
number of patients in exposed group. |
r |
allocation ratio (relative size of unexposed and exposed cohort
( |
conf.width |
precision (the full width of the confidence interval). |
conf.level |
confidence level. |
method |
Exactly one of |
... |
other arguments to uniroot (e.g. |
Details
Exactly one of the parameters n1 or conf.width must be passed as NULL,
and that parameter is determined from the other.
Woolf (woolf), Gart (gart), and Independence-smoothed logit
(indip_smooth) belong to a general family of adjusted confidence
intervals, adding 0 (woolf) to each cell, 0.5 (gart) to each cell, or an
adjustment for each cell based on observed data (independence-smoothed). In
gart and indip_smooth, estimate of the CI is not possible if p1 = 0, in
which case the OR becomes 0, but the lower level of the CI is > 0. Further,
if p1 = 1 and p2 < 1, or if p1 > 0 and p2 = 0, the OR
becomes \infty, but the upper limit of the CI is finite. For the
approximate intervals, gart and indip_smooth are the
recommended intervals (Fagerland et al. 2011).
uniroot is used to solve n for the woolf, gart, and
indip_smooth method.
Value
Object of class "presize", a list of arguments (including the computed one) augmented with method and note elements.
References
Fagerland MW, Lydersen S, Laake P (2015). Recommended confidence intervals for two independent binomial proportions. Statistical Methods in Medical Research, 24(2):224-254. doi:10.1177/0962280211415469.
Examples
# 10\% events in one group, 15\% in the other, 200 participants total
# (= 100 in each group), estimate confidence interval width
prec_or(p1 = .1, p2 = .15, n1 = 200/2)
# formula by Gart
prec_or(p1 = .1, p2 = .15, n1 = 200/2, method = "gart")
# formula by Woolf
prec_or(p1 = .1, p2 = .15, n1 = 200/2, method = "woolf")
# 10\% odds in one group, 15\% in the other, desired CI width of 0.1,
# estimate N
prec_or(p1 = .1, p2 = .15, conf.width = .1)
# formula by Gart
prec_or(p1 = .1, p2 = .15, conf.width = .1, method = "gart")
# formula by Woolf
prec_or(p1 = .1, p2 = .15, conf.width = .1, method = "woolf")
Sample size or precision for a proportion
Description
prec_prop returns the sample size or the precision for the provided
proportion.
Usage
prec_prop(
p,
n = NULL,
conf.width = NULL,
conf.level = 0.95,
method = c("wilson", "agresti-coull", "exact", "wald"),
...
)
Arguments
p |
proportion. |
n |
number of observations. |
conf.width |
precision (the full width of the confidence interval). |
conf.level |
confidence level. |
method |
The method to use to calculate precision. Exactly one method may be provided. Methods can be abbreviated. |
... |
other arguments to uniroot (e.g. |
Details
Exactly one of the parameters n or conf.width must be passed as NULL,
and that parameter is determined from the other.
The wilson, agresti-coull, exact, and wald method are implemented. The
wilson method is suggested for small n (< 40), and the agresti-coull method
is suggested for larger n (see reference). The wald method is not suggested,
but provided due to its widely distributed use.
uniroot is used to solve n for the agresti-coull,
wilson, and exact methods. Agresti-coull can be abbreviated by ac.
Value
Object of class "presize", a list of arguments (including the
computed one) augmented with method and note elements. In the wilson and
agresti-coull formula, the p from which the confidence interval is
calculated is adjusted by a term (i.e. p + term \pm ci). This
adjusted p is returned in padj.
References
Brown LD, Cai TT, DasGupta A (2001) Interval Estimation for a Binomial Proportion, Statistical Science, 16:2, 101-117, doi:10.1214/ss/1009213286
See Also
binom.test, binom.confint
in package binom, and binconf in package
Hmisc
Examples
# CI width for 15\% with 50 participants
prec_prop(0.15, n = 50)
# number of participants for 15\% with a CI width of 0.2
prec_prop(0.15, conf.width = 0.2)
# confidence interval width for a range of scenarios between 10 and 90\% with
# 100 participants via the wilson method
prec_prop(p = 1:9 / 10, n = 100, method = "wilson")
# number of participants for a range of scenarios between 10 and 90\% with
# a CI of 0.192 via the wilson method
prec_prop(p = 1:9 / 10, conf.width = .192, method = "wilson")
Sample size or precision for a rate
Description
prec_rate returns the sample size or the precision for the provided
rate.
Usage
prec_rate(
r,
x = NULL,
conf.width = NULL,
conf.level = 0.95,
method = c("score", "vs", "exact", "wald"),
...
)
Arguments
r |
rate or rate ratio. |
x |
number of events. |
conf.width |
precision (the full width of the confidence interval).
Should not exceed 5 times |
conf.level |
confidence level. |
method |
The method to use to calculate precision. Exactly one method may be provided. Methods can be abbreviated. |
... |
other arguments to uniroot (e.g. |
Details
Exactly one of the parameters r or conf.width must be passed as NULL,
and that parameter is determined from the other.
The score, variance stabilizing (vs), exact, and
wald method are implemented to calculate the rate and the precision.
For few events x (<5), the exact method is recommended.
If more than one method is specified or the method is miss-specified, the 'score' method will be used.
uniroot is used to solve n for the score and
exact method.
Value
Object of class "presize", a list of arguments (including the computed one) augmented with method and note elements.
References
Barker, L. (2002) A Comparison of Nine Confidence Intervals
for a Poisson Parameter When the Expected Number of Events is \le 5,
The American Statistician, 56:2, 85-89,
doi:10.1198/000313002317572736
See Also
Examples
# confidence interval width for a rate of 2.5 events per unit and 20 events,
# using the score method
prec_rate(2.5, x = 20, met = "score")
# number of events to yield a CI width of 2.243 for a rate of 2.5 events per
# unit and 20 events, using the score method
prec_rate(2.5, conf.width = 2.243, met = "score")
# confidence interval width for a rate of 2.5 events per unit and 20 events,
# using the exact method
prec_rate(2.5, x = 20, met = "exact")
# vs and wald have the same conf.width, but different lwr and upr
prec_rate(2.5, x = 20, met = "vs")
prec_rate(2.5, x = 20, met = "wald")
Sample size or precision for a rate ratio
Description
prec_rateratio returns the sample size or the precision for the
provided proportions.
Usage
prec_rateratio(
n1 = NULL,
rate1 = NULL,
rate2 = 2 * rate1,
prec.level = NULL,
r = 1,
conf.level = 0.95
)
Arguments
n1 |
number of patients in exposed group. |
rate1 |
event rate in the exposed group. |
rate2 |
event rate in the unexposed group. |
prec.level |
ratio of the upper limit over the lower limit of the rate ratio confidence interval. |
r |
allocation ratio (relative size of unexposed and exposed cohort
( |
conf.level |
confidence level. |
Details
Exactly one of the parameters n1 or conf.width must be passed as
NULL, and that parameter is determined from the other. Event rates in the two
groups should also be provided (rate1, rate2). If only
rate1 is provided, rate2 is assumed to be 2 times
rate1.
References
Rothman KJ, Greenland S (2018). Planning Study Size Based on Precision Rather Than Power. Epidemiology, 29:599-603. doi:10.1097/EDE.0000000000000876.
Examples
# 20 participants, a rate of 50% against a rate of 300\%
prec_rateratio(20, .5, 3)
# sample size required to attain a CI whose upper limit is not more than 3.81 larger
# than the lower limit
prec_rateratio(rate1 = .5, rate2 = 3, prec.level = 3.81)
Sample size or precision for risk difference
Description
prec_riskdiff returns the risk difference and the sample size or the
precision for the provided proportions.
Usage
prec_riskdiff(
p1,
p2,
n1 = NULL,
conf.width = NULL,
r = 1,
conf.level = 0.95,
method = c("newcombe", "mn", "ac", "wald"),
...
)
Arguments
p1 |
risk among exposed. |
p2 |
risk among unexposed. |
n1 |
number of patients in exposed group. |
conf.width |
precision (the full width of the confidence interval). |
r |
allocation ratio (relative size of exposed and unexposed cohort
( |
conf.level |
confidence level. |
method |
Exactly one of |
... |
other options to uniroot (e.g. |
Details
Exactly one of the parameters n1 or conf.width must be passed as NULL,
and that parameter is determined from the other.
Newcombe (newcombe) proposed a confidence interval based on the wilson
score method for the single proportion (see prec_prop). The confidence
interval without continuity correction is implemented from equation 10 in
Newcombe (1998).
Miettinen-Nurminen (mn) provide a closed from equation for the
restricted maximum likelihood estimate . The implementation is based on
code provided by Yongyi Min on
https://users.stat.ufl.edu/~aa/cda/R/two-sample/R2/index.html.
Agresti-Caffo (ac) confidence interval is based on the Wald confidence
interval, adding 1 success to each cell of the 2 x 2 table (see Agresti and
Caffo 2000).
uniroot is used to solve n for the newcombe, ac, and mn
method.
References
Agresti A (2003) Categorical Data Analysis, Second Edition, Wiley Series in Probability and Statistics, doi:10.1002/0471249688.
Agresti A and Caffo B (2000) Simple and Effective Confidence Intervals for Proportions and Differences of Proportions Result from Adding Two Successes and Two Failures, The American Statistician, 54(4):280-288.
Miettinen O and Nurminen M (1985) Comparative analysis of two rates, Statistics in Medicine, 4:213-226.
Newcombe RG (1998) Interval estimation for the difference between independent proportions: comparison of eleven methods, Statistics in Medicine, 17:873-890.
Fagerland MW, Lydersen S, and Laake P (2015). Recommended confidence intervals for two independent binomial proportions, Statistical methods in medical research 24(2):224-254.
Examples
# proportions of 40 and 30\%, 50 participants, how wide is the CI?
prec_riskdiff(p1 = .4, p2 = .3, n1 = 50)
# proportions of 40 and 30\%, 50 participants, how many participants for a CI 0.2 wide?
prec_riskdiff(p1 = .4, p2 = .3, conf.width = .2)
# Validate Newcombe (1998)
prec_riskdiff(p1 = 56/70, p2 = 48/80, n1 = 70, r = 70/80, met = "newcombe") # Table IIa
prec_riskdiff(p1 = 10/10, p2 = 0/10, n1 = 10, met = "newcombe") # Table IIh
# multiple scenarios
prec_riskdiff(p1 = c(56/70, 9/10, 6/7, 5/56),
p2 = c(48/80, 3/10, 2/7, 0/29),
n1 = c(70, 10, 7, 56),
r = c(70/80, 1, 1, 56/29),
method = "wald")
Sample size or precision for risk ratio
Description
prec_riskratio returns the risk ratio and the sample size or the
precision for the provided proportions.
Usage
prec_riskratio(
p1,
p2,
n1 = NULL,
r = 1,
conf.width = NULL,
conf.level = 0.95,
method = c("koopman", "katz"),
...
)
Arguments
p1 |
risk among exposed. |
p2 |
risk among unexposed. |
n1 |
number of patients in exposed group. |
r |
allocation ratio (relative size of unexposed and exposed cohort
( |
conf.width |
precision (the full width of the confidence interval). |
conf.level |
confidence level. |
method |
Exactly one of |
... |
other arguments to uniroot (e.g. |
Details
Exactly one of the parameters n1 or conf.width must be passed as NULL,
and that parameter is determined from the other.
Koopman (koopman) provides an asymptotic score confidence interval
that is always consistent with Pearsons chi-squared test. It is the
recommended interval (Fagerland et al.).
Katz (katz) use a logarithmic transformation to calculate the
confidence interval. The CI cannot be computed if one of the proportions is
zero. If both proportions are 1, the estimate of the standard error becomes
zero, resulting in a CI of [1, 1].
uniroot is used to solve n for the katz, and koopman
method.
References
Fagerland MW, Lydersen S, and Laake P (2015). Recommended confidence intervals for two independent binomial proportions, Statistical methods in medical research 24(2):224-254.
Katz D, Baptista J, Azen SP, and Pike MC (1978) Obtaining Confidence Intervals for the Risk Ratio in Cohort Studies, Biometrics 34:469-474.
Koopman PAR (1984) Confidence Intervals for the Ratio of Two Binomial Proportions, Biometrics 40:513-517.
Examples
# Validate function with example in Fagerland et al. (2015), Table 5.
prec_riskratio(p1 = 7/34, p2 = 1/34, n1 = 34, r = 1, met = "katz")
# 7 (0.91 to 54)
prec_riskratio(p1 = 7/34, p2 = 1/34, n1 = 34, r = 1, met = "koopman")
# 7 (1.21 to 43)
# Validate the Koopman method with example in Koopman (1984)
prec_riskratio(p1 = 36/40, p2 = 16/80, n1 = 40, r = 2, met = "koopman")
# 4.5 (2.94 to 7.15)
Sample size and precision of sensitivity and specificity
Description
Because sensitivity (true positives/total number of positives) and specificity (true
negatives/total number of negatives) are simple proportions, these
functions act as wrappers for prec_prop.
Usage
prec_sens(
sens,
n = NULL,
ntot = NULL,
prev = NULL,
conf.width = NULL,
round = "ceiling",
...
)
prec_spec(
spec,
n = NULL,
ntot = NULL,
prev = NULL,
conf.width = NULL,
round = "ceiling",
...
)
Arguments
sens, spec |
proportions. |
n |
number of observations. |
ntot |
total sample size. |
prev |
prevalence of cases/disease (i.e. proportion of |
conf.width |
precision (the full width of the confidence interval). |
round |
string, round calculated |
... |
options passed to prec_prop (e.g. method, conf.width, conf.level). |
Details
If ntot and prev are given, they are used to calculate
n.
Value
Object of class "presize", a list of arguments (including the computed one) augmented with method and note elements.
Note
Calculated n can take on non-integer numbers, but
prec_prop requires integers, so the calculated n is rounded
according to the approach indicated in round.
See Also
prec_prop
Examples
# confidence interval width with n
prec_sens(.6, 50)
# confidence interval width with ntot and prevalence (assuming 50% prev)
prec_sens(.6, ntot = 100, prev = .5)
# sample size with confidence interval width
prec_sens(.6, conf.width = 0.262)